New Square Root Algorithm
"The Successive Reduction Method"
by
Namir C. Shammas
This article discusses a new algorithm that calculates square roots. I will call this new method the Successive Reduction method. As you will see later, this method works for any root and not just square root values.
The most popular algorithm to calculate square roots using basic mathematical operations is the one based on Newton's method. This algorithm uses the following basic guess-refining equation:
X' = (N / X + X) / 2
Where N is the square, X is the old guess for the square root, and X' is the new guess for the square root.
The new algorithm is based on success reduction of the guess for the square root. The algorithm is aimed at squares of numbers greater than 1. In the case of numbers smaller than 1, you work with the reciprocal of the square. Once you calculate the square root you then return its reciprocal value to get the answer.
The pseudo code for the Successive Reduction method is:
Given: a square N.
The success of the Successive-Reduction method lies in the calculations involved in updating the factor F that is used to divide the guess for the square root. This division scheme reduces the guess for the square root until it approaches the actual square root, within accepted tolerance. As the guess for the square root approaches the actual value, the reduction factor approaches 1.
Selecting the initial value of the factor F and the scheme to reduce it affects the number of iterations. The first aspect in this scheme is selecting the initial value of the factor F. Experimenting with the algorithm showed that the initial value of 16 is adequate. You may choose a higher or lower value, since 16 is not etched in stone. What about reducing the values for F? Early experimentation with the algorithm showed that using the following equation gave a good sequence of values for F that remained above 1:
| F = F^0.5 | ... (1) |
Of course using the square root function with F to calculator the square root of any other number is not acceptable. Since most of the values of F are close to F, the first acceptable variation of the above equation uses the following approximation:
| F = 1 + (F - 1) / 2 | ... (2) |
which is based on the approximation:
(1 + X)^0.5 = 1 + X/2
I also experimented with expressions like:
| F = 1 + (F - 1) * 0.75 | ... (3) |
And,
| F = 1 + (F - 1) * 0.95 | ... (4) |
Higher values used to multiply with (F - 1) reduced the number of outer iterations, but increased the number of inner iterations (represented by step 6). Using a gradual shift, based on the number of iterations I gives forms like the next one:
| F = 1 + (F - 1) * (0.50 + 0.45 / I) | ... (5) |
The above equation gradually reduces the value of F as the number of inner iterations increases. I will call this scheme Method 1. I also used another approach that uses the form:
| F = 1 + (F - 1) *K | ... (6) |
Where K remains constant for a specific number of iterations. The algorithm decreases the value for K in a stepwise manner. I will call this scheme for altering the values of F, Method 2.
To reduce the number of calculations, I created classes that pre-calculate arrays that store the sequence of the values of factor F. This approach allows each class to initially calculate the sequence of F values (which is independent of the square value) and reuse it for as many times the class instances calculate square roots.
Here is a table that compares the Method 1 scheme, the Method 2 scheme, and Newton's method. All methods use the same tolerance value of 0.00000000001.
|
Square |
Square Root |
Outer Iterations Method 1 / Method 2 |
Inner Iterations Method 1 / Method 2 |
Iterations Using Newton's Method |
|
10 |
3.16227766015479 |
16/11 |
46/99 |
7 |
|
100 |
10 |
14/13 |
46/99 |
9 |
|
1000 |
31.6227766017003 |
21/14 |
46/99 |
11 |
|
10000 |
100 |
22/13 |
46/99 |
12 |
|
1E5 |
316.227766017003 |
18/14 |
46/99 |
14 |
|
1E6 |
1000 |
18/15 |
46/99 |
16 |
|
1E7 |
3162.27766017003 |
18/12 |
46/99 |
17 |
|
1E8 |
10000 |
21/16 |
46/99 |
19 |
|
1E9 |
31622.7766017003 |
23/16 |
46/99 |
21 |
|
1E10 |
100000 |
19/17 |
46/99 |
22 |
|
14400 |
120 |
15/11 |
46/99 |
13 |
|
68943 |
262.569990669163 |
16/14 |
46/99 |
14 |
Looking at the data in the above table, you can see that Newton's method requires fewer iterations to calculate the square root for smaller squares. The Success Reduction method (in particular Method 2) does better than Newton's method for higher squares. Using pre-calculated arrays of factors speeds up the inner iterations since the code is recalling values instead of calculating them. The table also shows that the number of inner loop iterations remains steady for both methods, regardless of the value of the square.
Here is the VBA source code for an Excel file that implements the new algorithm.
Option Explicit Sub CalcSqrtMethod1() ' Uses Method1 scheme for reducing the division factor Dim objSqrt As CSqrt1 Dim objNewton As CNewton Set objNewton = New CNewton Set objSqrt = New CSqrt1 objSqrt.Calc Sheet1 ' perform Newton's method objNewton.CalcRoot Sheet1 End Sub Sub CalcSqrtMethod2() ' Uses Method1 scheme for reducing the division factor Dim objSqrt As CSqrt2 Dim objNewton As CNewton Set objNewton = New CNewton Set objSqrt = New CSqrt2 objSqrt.Calc Sheet1 ' perform Newton's method objNewton.CalcRoot Sheet1 End Sub
Here is the source code for class CSqrt1. Worthy of mention is the array FactorArr that stores the values for the reduction factor:
Option Explicit
Const TOLER = 0.00000000001
Const MAX_COEFF = 250
Const MAX_COEFF_INC = 10
Private FactorArr() As Double
Private MaxCoeff As Integer, NewMaxCoeff As Integer
Private Sub Class_Initialize()
Dim J As Integer
MaxCoeff = MAX_COEFF
ReDim FactorArr(MaxCoeff)
FactorArr(1) = 16
For J = 2 To MaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
End Sub
Private Sub ExpandFactorArray()
Dim J As Integer
NewMaxCoeff = MaxCoeff + MAX_COEFF_INC
ReDim Preserve FactorArr(NewMaxCoeff)
For J = MaxCoeff + 1 To NewMaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
MaxCoeff = NewMaxCoeff
End Sub
Public Sub Calc(sh As Worksheet)
Dim R As Integer
Dim SQRVAL As Double
Dim X As Double, X1 As Double, Diff As Double
Dim LastX As Double
Dim I As Integer, J As Integer
Dim bIsLessThanOne As Boolean
sh.Range("C1").Value = "X"
sh.Range("D1").Value = "F"
sh.Range("E1").Value = "I"
sh.Range("C2:Z10000").Value = ""
SQRVAL = sh.Cells(1, 2)
If SQRVAL = 1 Then
sh.Cells(2, 2) = 1
sh.Cells(3, 2) = 1
End If
bIsLessThanOne = SQRVAL < 1
If bIsLessThanOne Then SQRVAL = 1 / SQRVAL
R = 2
X = SQRVAL
I = 1
Do
LastX = X
X = X / FactorArr(I)
Do Until (X * X >= SQRVAL) Or ((FactorArr(I) - 1) <= TOLER)
I = I + 1
' IF statement not needed if size of array FactorArr is large enough
If I > MaxCoeff Then ExpandFactorArray
X = LastX / FactorArr(I)
Loop
sh.Cells(R, 3) = X
sh.Cells(R, 4) = FactorArr(I)
sh.Cells(R, 5) = I
R = R + 1
Loop Until (Abs(SQRVAL - X * X) <= TOLER) Or (FactorArr(I) - 1 <= TOLER) Or (X = LastX)
If bIsLessThanOne Then X = 1 / X
sh.Cells(2, 2) = X
sh.Cells(3, 2) = X ^ 2
End Sub
Here is the source code for class CSqrt2:
Option Explicit
Const TOLER = 0.00000000001
Const NUM_COEFF_IN_SET = 100
Const MAX_COEFF = 250
Const MAX_COEFF_INC = 10
Private FactorArr() As Double
Private MaxCoeff As Integer, NewMaxCoeff As Integer
Private Sub Class_Initialize()
Dim J As Integer, I As Integer
Dim X As Double
MaxCoeff = MAX_COEFF
ReDim FactorArr(MaxCoeff)
FactorArr(1) = 16
I = 0
X = 0.75
For J = 2 To MaxCoeff
I = I + 1
If I Mod NUM_COEFF_IN_SET = 0 Then
I = 1
X = X - 0.1
If X < 0.5 Then X = 0.5
End If
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * X
Next J
End Sub
Private Sub ExpandFactorArray()
Dim J As Integer
NewMaxCoeff = MaxCoeff + MAX_COEFF_INC
ReDim Preserve FactorArr(NewMaxCoeff)
For J = MaxCoeff + 1 To NewMaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
MaxCoeff = NewMaxCoeff
End Sub
Public Sub Calc(sh As Worksheet)
Dim R As Integer
Dim SQRVAL As Double
Dim X As Double, X1 As Double, Diff As Double
Dim LastX As Double
Dim I As Integer, J As Integer
Dim bIsLessThanOne As Boolean
sh.Range("C1").Value = "X"
sh.Range("D1").Value = "F"
sh.Range("E1").Value = "I"
sh.Range("C2:Z10000").Value = ""
SQRVAL = sh.Cells(1, 2)
If SQRVAL = 1 Then
sh.Cells(2, 2) = 1
sh.Cells(3, 2) = 1
End If
bIsLessThanOne = SQRVAL < 1
If bIsLessThanOne Then SQRVAL = 1 / SQRVAL
R = 2
X = SQRVAL
I = 1
Do
LastX = X
X = X / FactorArr(I)
Do Until (X * X >= SQRVAL) Or ((FactorArr(I) - 1) <= TOLER)
I = I + 1
' IF statement not needed if size of array FactorArr is large enough
If I > MaxCoeff Then ExpandFactorArray
X = LastX / FactorArr(I)
Loop
sh.Cells(R, 3) = X
sh.Cells(R, 4) = FactorArr(I)
sh.Cells(R, 5) = I
R = R + 1
Loop Until (Abs(SQRVAL - X * X) <= TOLER) Or (FactorArr(I) - 1 <= TOLER) Or (X = LastX)
If bIsLessThanOne Then X = 1 / X
sh.Cells(2, 2) = X
sh.Cells(3, 2) = X ^ 2
End Sub
Here is the source code for class CNewton that applies Newton's method:
Option Explicit
Public Sub CalcRoot(sh As Worksheet)
Dim X As Double, LastX As Double
Dim SQRVAL As Double
Dim R As Integer
SQRVAL = sh.Cells(1, 2)
sh.Range("G1").Value = "X (Newton)"
If SQRVAL = 1 Then
Range("G2").Value = 1
Exit Sub
End If
R = 2
X = SQRVAL / 2
Cells(R, 7) = X
Do
LastX = X
X = (SQRVAL / X + X) / 2
R = R + 1
sh.Cells(R, 7) = X
Loop Until X = LastX
End Sub
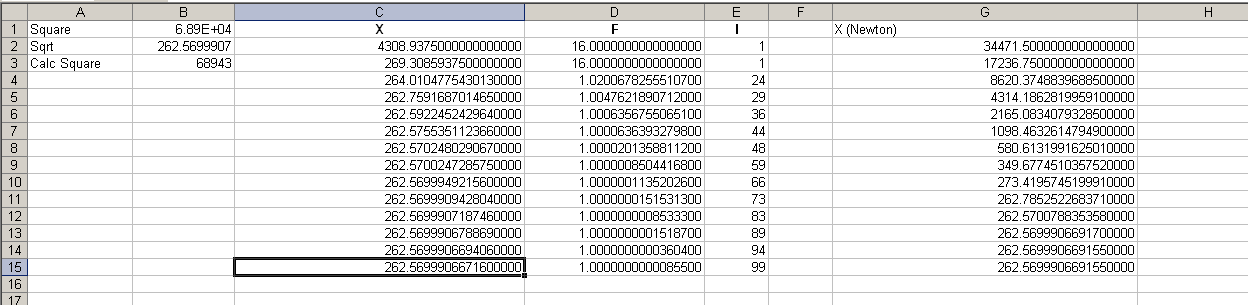
The following figure shows the Excel sheet with sample data:

The method of Successive Reduction can be easily adapted
for any positive integer and positive real root value.
Copyright (c) Namir Shammas. All rights reserved.