New Root Algorithm
"The Successive Reduction Method"
by
Namir C. Shammas
This article is a follow-up for the New Square Root Algorithm article. The latter article presented the Successive Reduction method as a technique to calculate square roots. This article discusses expanding the new algorithm to calculate any root and not just square root values.
Newton's method is the most popular algorithm to calculate general roots given by:
X^Y = N
Where N is the value that is equal to X raised to power Y. Using basic mathematical operations Newton's method is able to calculate X for a given set of values for N and Y. This algorithm uses the following basic guess-refining equation:
X' = N /(Y * X^(Y-1)) + (Y-1)/Y * X
This article shows you how to extend he Successive Reduction method to solve the first equation.
The pseudo code for the Successive Reduction method is:
Given: a value N and power Y.
In the above pseudo-code I am using X^Y as a short hand for chained multiplication of X.
The success of the Successive-Reduction method lies in the calculations involved in updating the factor F that is used to divide the guess for the root. This division scheme reduces the guess for the root until it approaches the actual root, within accepted tolerance. As the guess for the root approaches the actual value, the reduction factor approaches 1.
I used the same schemes involved in calculating the square roots.
Here is a table that compares the Method 1 scheme, the Method 2 scheme, and Newton's method. All methods use the same tolerance value of 0.00000000001.
|
Value |
Power |
Root |
Outer Iterations Method 1 / Method 2 |
Inner Iterations Method 1 / Method 2 |
Iterations Using Newton's Method |
|
100 |
2 |
10 |
14/13 |
46/99 |
9 |
|
1000 |
3 |
10 |
22/13 |
46/99 |
16 |
|
10000 |
4 |
10 | 18/15 | 46/99 | 27 |
|
14400 |
3 |
24.3288079823695 |
20/12 |
46/99 |
20 |
|
123456 |
3 |
49.7932798465802 |
20/15 |
46/99 |
23 |
|
123456 |
4 |
18.7446808480133 |
24/14 |
46/99 |
34 |
|
123456 |
5 |
10.4304354640421 |
22/13 |
46/99 |
42 |
|
1E6 |
6 |
10 |
19/17 |
46/99 |
60 |
|
1E6 |
4.5 |
21.5544790236265 |
19/14 |
46/99 |
44 |
|
1E6 |
3.5 |
51.7947467920397 |
24/16 |
46/99 |
33 |
Looking at the data in the above table, you can see that Newton's method requires fewer iterations to calculate smaller roots for smaller values. The Success Reduction method (in particular Method 2) does much better than Newton's method for higher roots of higher values of N. Using pre-calculated arrays of factors speeds up the inner iterations since the code is recalling values instead of calculating them. The table also shows that the number of inner loop iterations remains steady for both methods, regardless of the value of N.
Here is the VBA source code for an Excel file that implements the new algorithm.
Option Explicit Sub CalcRoot1() Dim objRoot As CRoot1 Dim objNewton As CNewton Set objNewton = New CNewton Set objRoot = New CRoot1 objRoot.Calc Sheet1 ' perform Newton's method objNewton.CalCRoot Sheet1 End Sub Sub CalcRoot2() Dim objRoot As CRoot2 Dim objNewton As CNewton Set objNewton = New CNewton Set objRoot = New CRoot2 objRoot.Calc Sheet1 ' perform Newton's method objNewton.CalCRoot Sheet1 End Sub
Here is the source code for class CRoot1. Worthy of mention is the array FactorArr that stores the values for the reduction factor:
Option Explicit
Const TOLER = 0.00000000001
Const MAX_COEFF = 250
Const MAX_COEFF_INC = 10
Private FactorArr() As Double
Private MaxCoeff As Integer, NewMaxCoeff As Integer
Private Sub Class_Initialize()
Dim J As Integer
MaxCoeff = MAX_COEFF
ReDim FactorArr(MaxCoeff)
FactorArr(1) = 16
For J = 2 To MaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
End Sub
Private Sub ExpandFactorArray()
Dim J As Integer
NewMaxCoeff = MaxCoeff + MAX_COEFF_INC
ReDim Preserve FactorArr(NewMaxCoeff)
For J = MaxCoeff + 1 To NewMaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
MaxCoeff = NewMaxCoeff
End Sub
Public Sub Calc(sh As Worksheet)
Dim R As Integer
Dim SQRVAL As Double
Dim X As Double, X1 As Double, Diff As Double
Dim LastX As Double, Power As Double
Dim I As Integer, J As Integer
Dim bIsLessThanOne As Boolean
sh.Range("C1").Value = "X"
sh.Range("D1").Value = "F"
sh.Range("E1").Value = "I"
sh.Range("C2:Z10000").Value = ""
SQRVAL = sh.Cells(1, 2)
If SQRVAL = 1 Then
sh.Cells(2, 2) = 1
sh.Cells(3, 2) = 1
End If
Power = sh.Cells(2, 2)
bIsLessThanOne = SQRVAL < 1
If bIsLessThanOne Then SQRVAL = 1 / SQRVAL
R = 2
X = SQRVAL
I = 1
Do
LastX = X
X = X / FactorArr(I)
Do Until (X ^ Power >= SQRVAL) Or ((FactorArr(I) - 1) <= TOLER)
I = I + 1
' IF statement not needed if size of array FactorArr is large enough
If I > MaxCoeff Then ExpandFactorArray
X = LastX / FactorArr(I)
Loop
sh.Cells(R, 3) = X
sh.Cells(R, 4) = FactorArr(I)
sh.Cells(R, 5) = I
R = R + 1
Loop Until (Abs(SQRVAL - X ^ Power) <= TOLER) Or (FactorArr(I) - 1 <= TOLER) Or (X = LastX)
If bIsLessThanOne Then X = 1 / X
sh.Cells(3, 2) = X
sh.Cells(4, 2) = X ^ Power
End Sub
Here is the source code for class CRoot2:
Option Explicit
Const TOLER = 0.00000000001
Const NUM_COEFF_IN_SET = 100
Const MAX_COEFF = 250
Const MAX_COEFF_INC = 10
Private FactorArr() As Double
Private MaxCoeff As Integer, NewMaxCoeff As Integer
Private Sub Class_Initialize()
Dim J As Integer, I As Integer
Dim X As Double
MaxCoeff = MAX_COEFF
ReDim FactorArr(MaxCoeff)
FactorArr(1) = 16
I = 0
X = 0.75
For J = 2 To MaxCoeff
I = I + 1
If I Mod NUM_COEFF_IN_SET = 0 Then
I = 1
X = X - 0.1
If X < 0.5 Then X = 0.5
End If
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * X
Next J
End Sub
Private Sub ExpandFactorArray()
Dim J As Integer
NewMaxCoeff = MaxCoeff + MAX_COEFF_INC
ReDim Preserve FactorArr(NewMaxCoeff)
For J = MaxCoeff + 1 To NewMaxCoeff
FactorArr(J) = 1 + (FactorArr(J - 1) - 1) * (0.5 + 0.45 / J)
Next J
MaxCoeff = NewMaxCoeff
End Sub
Public Sub Calc(sh As Worksheet)
Dim R As Integer
Dim SQRVAL As Double
Dim X As Double, X1 As Double, Diff As Double
Dim LastX As Double, Power As Double
Dim I As Integer, J As Integer
Dim bIsLessThanOne As Boolean
sh.Range("C1").Value = "X"
sh.Range("D1").Value = "F"
sh.Range("E1").Value = "I"
sh.Range("C2:Z10000").Value = ""
SQRVAL = sh.Cells(1, 2)
If SQRVAL = 1 Then
sh.Cells(2, 2) = 1
sh.Cells(3, 2) = 1
End If
Power = sh.Cells(2, 2)
bIsLessThanOne = SQRVAL < 1
If bIsLessThanOne Then SQRVAL = 1 / SQRVAL
R = 2
X = SQRVAL
I = 1
Do
LastX = X
X = X / FactorArr(I)
Do Until (X ^ Power >= SQRVAL) Or ((FactorArr(I) - 1) <= TOLER)
I = I + 1
' IF statement not needed if size of array FactorArr is large enough
If I > MaxCoeff Then ExpandFactorArray
X = LastX / FactorArr(I)
Loop
sh.Cells(R, 3) = X
sh.Cells(R, 4) = FactorArr(I)
sh.Cells(R, 5) = I
R = R + 1
Loop Until (Abs(SQRVAL - X ^ Power) <= TOLER) Or (FactorArr(I) - 1 <= TOLER) Or (X = LastX)
If bIsLessThanOne Then X = 1 / X
sh.Cells(3, 2) = X
sh.Cells(4, 2) = X ^ 2
End Sub
Here is the source code for class CNewton that applies Newton's method:
Option Explicit
Public Sub CalCRoot(sh As Worksheet)
Dim X As Double, LastX As Double
Dim SQRVAL As Double, Power As Double
Dim R As Integer
SQRVAL = sh.Cells(1, 2)
sh.Range("G1").Value = "X (Newton)"
If SQRVAL = 1 Then
Range("G2").Value = 1
Exit Sub
End If
Power = sh.Cells(2, 2)
R = 2
X = SQRVAL / Power
Cells(R, 7) = X
Do
LastX = X
X = SQRVAL / Power / X ^ (Power - 1) + (Power - 1) / Power * X
R = R + 1
sh.Cells(R, 7) = X
Loop Until X = LastX
End Sub
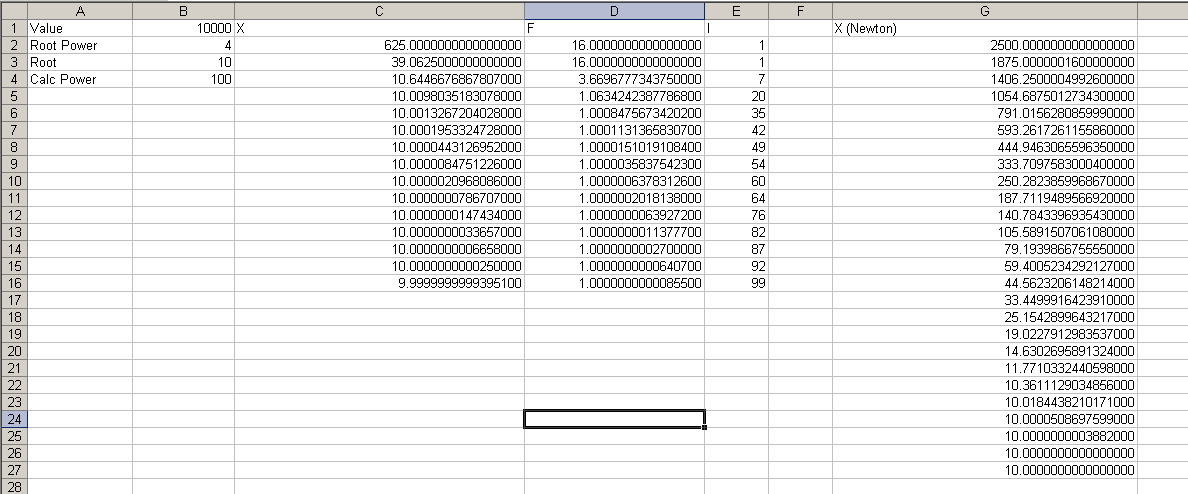
The following figure shows the Excel sheet with sample data:

Copyright (c) Namir Shammas. All rights reserved.